Функции и их графики. Преобразования графиков функций.

Функции и их графики

Функция f  — это правило, согласно которому каждому элементу x из множества X ставится в соответствие единственный элемент y из множества Y.

Если элементу сопоставлен элемент , то говорят, что элемент y находится в функциональной зависимости f от элемента x. При этом переменная x называется аргументом функции f или независимой переменной, множество X называется областью задания или областью определения функции, а элемент y, соответствующий конкретному элементу x — частным значением функции f в точке x. Множество Y всех возможных частных значений функции f называется её областью значений или областью изменения.


График функции — множество точек, у которых абсциссы являются допустимыми значениями аргумента x, а ординаты — соответствующими значениями функциии y.
Обычно рассматриваются графики вещественных скалярных функций одного вещественного переменного 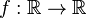, которые являются множеством точек плоскости .

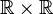Преобразования графиков функций

Общий вид функции	Преобразования
y = f(x − a)	Параллельный перенос графика вдоль оси абсцисс на | a | единиц вправо, если a > 0; влево, если a < 0.
y = f(x) + a	Параллельный перенос графика вдоль оси ординат на | a | единиц вверх, если a > 0, вниз, если a < 0.
y = f( − x)	Симметричное отражение графика относительно оси ординат.
y = − f(x)	Симметричное отражение графика относительно оси абсцисс.
y = f(kx)	При k > 1 — сжатие графика к оси ординат в k раз, при 0 < k < 1 — растяжение графика от оси ординат в 1 / k раз.
y = kf(x)	При k > 1 — растяжение графика от оси абсцисс в k раз, при 0 < k < 1 — cжатие графика к оси абсцисс в 1 / k раз.
y = | f(x) |	При — график остаётся без изменений, при f(x) < 0 — график симметрично отражается относительно оси абсцисс.
y = f( | x | )	При — график остаётся без изменений, при x < 0 — график симметрично отражается относительно оси ординат.